Piste rouge

Probabilité

"Nous devons envisager l'état présent de l'univers comme l'effet de son état antérieur et comme la cause de celui qui va suivre. Une intelligence qui, pour un instant donné, connaîtrait toutes les forces dont la nature est animée et la situation respective des êtres qui la composent, si d'ailleurs elle était assez vaste pour soumettre ces données à l'analyse, embrasserait dans la même formule les mouvements des plus grands corps de l'univers et ceux du plus léger atome; rien ne serait incertain pour elle, et l'avenir, comme le passé, serait présent à ses yeux."

Laplace

Avec les relations d’incertitudes d’Heisenberg et les lois du chaos, on ne croit pas aujourd’hui pouvoir prédire l’ensemble des phénomènes de l’univers. Les théories actuelles demeurent une bonne approximation, mais il semblerait qu’il restera toujours un pourcentage de phénomène non explicable, des « accidents ».

Ainsi, nous devons nous en remettre aux probabilités. C’est ce que fait la physique quantique. Elle ne prédit pas, par exemple, que nous trouverons l’électron à un endroit précis autour de l’atome, elle dit que dans 80 % des cas, nous le trouverons dans un endroit quelconque, dans 10 % des cas, dans un autre endroit, etc. La fonction qui évalue ces probabilités s’appelle la fonction de densité de probabilité.

Ex 1 : Planche de Galton

Plusieurs billes tombent au travers d’une pyramide de clous. En frappant chaque clou, chacune des billes a une chance sur deux de tomber d’un côté ou de l’autre. Quelle est la fonction de densité de probabilité de ce problème ?

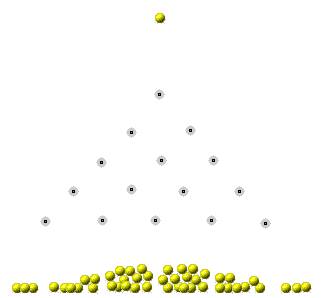
Cette pyramide de clous s’appelle une planche de Galton. Nous constatons avec l’observation que ce problème possède une densité de probabilité distribuée sous la forme d’une courbe en cloche. Nous appelons ce type de courbe une gaussienne et la distribution s'y rapportant, une distribution normale.

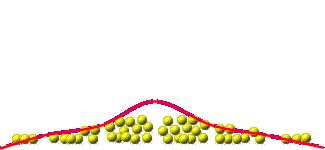
La planche de Galton suit une loi binomiale. Les probabilités que la bille tombe dans une case ou l’autre se calculent ainsi :

p(x) = probabilité
n = nombre d’essais
x = nombre de succès
p = probabilité de succès

p(x) = (	n	) p^x(1-p) ^n-x pour x = 0,1,2,...,n où
	x

(

) =

n x (n-1) x (n-2) x...x (n-x-1)

x x (x-1) x (x-2) x...x 1

pour x = 0,1,...,n

Ainsi, dans l’exemple illustré, la bille tombe au travers de 5 étages de clous (n = 5). La probabilité que la bille tombe dans la case à l’extrême gauche (x = 5) est de :

p(x) = 0,5⁵ (1-0,5)^5-5 = 0,03125 = 3,13 %

Qu’elle tombe dans la deuxième case à partir de la gauche :

p(x) = (5) 0,5⁴ (1-0,5)^5-4 = 15,63 %

Et qu’elle tombe dans les 2 cases du centre :

p(x) = [(5 x 4) / (2 x 1)] 0,5³ (1-0,5)^5-3 = 31,25 %

Le graphique de densité de probabilité (F(x)) en fonction de x (nombre de fois que la bille tombe à gauche) donne ceci :

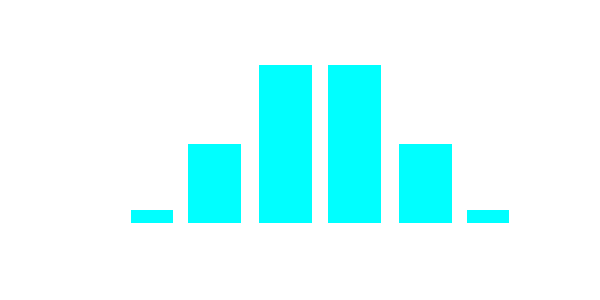
La somme totale doit toujours donner 100 %. Nous voyons que c’est le cas ici. De plus, on voit que si nous faisons tendre n vers un chiffre de plus en plus grand, la distribution s’apparente à une gaussienne. C’est une conséquence du théorème central limite (TCL). C’est l’un des plus fameux et des plus importants théorème en statistique.

Ex 2 : Les singes

Supposons que 10 milliards de singes tapent sur 10 milliards de machines à écrire pendant un temps équivalent à l’âge de l’univers (10¹⁸ secondes) et à un rythme de 10 touches/secondes, quelle est la probabilité que ces singes écrivent au hasard Hamlet de Shakespeare (100 000 caractères) si un clavier contient environ 44 caractères (sans distinguer les majuscules et les minuscules) ?

Tout d’abord, il faut savoir la probabilité de taper une séquence de 100 000 caractères au hasard. Si un clavier compte 44 touches, nous avons donc une chance sur 44 de taper le caractère approprié à chaque essai.

Ainsi :

1/44 (1^ière touche) x 1/44 (2^ième touche) x 1/44 (3^ième touche) x …. x 1/44 (100 000^ième touche)

Donc, la probabilité est de 1 / 44^{100 000}= 10^-164 345

Maintenant, voyons quelle est la chance des singes :

10 milliards de singes x 10 touches / secondes x 10¹⁸ secondes = 10²⁹

Finalement, la chance que les 10 milliards de singes tapent au hasard Hamlet est de :

10²⁹ / 10^164 345 = 10^-164 316

D’ailleurs, cet exemple nous amène à parler des cas où les statistiques ne peuvent pas s’appliquer. Les statistiques sont utilisées pour évaluer des événements reproductibles et non uniques. Par exemple, si vous essayez d’évaluer la probabilité de votre existence, vous arriverez à une probabilité presque nulle ! Par exemple, on évaluerait la probabilité que vous soyez une fille, que vous ayez les cheveux bruns, les yeux noirs, un point de beauté à 18,4569 cm du bas de votre cou et à 7,5654 cm du côté droit, un poils à 4,560 mm du bas de la cheville, un autre à 5,891 mm en diagonale du précédent, etc. Si nous vous décrivons suffisamment précisément, on en arrive à la quasi-impossibilité, au niveau des probabilités, de votre existence. C’est pourquoi il faut faire attention avant d’utiliser les probabilités pour décrire tous les phénomènes nous environnant. Ce point est à ne pas négliger pour la recherche SETI. Si nous décrivons tous les détails qui ont fait en sorte que la vie intelligente apparaisse, nous obtenons une probabilité presque nulle d’apparition. Or, nous existons. Nous sommes donc la preuve que les probabilités ne semblent pas appropriées pour évaluer la chance d’apparition de la vie complexe.

Commentaires ? Suggestions ? Infarctus ? Écrivez-les moi à svilleneuve@cegep-chicoutimi.qc.ca

Références

LESSARD, S. et MONGA : « Statistique : concepts et méthodes », Éditions Masson, 1993, p 198-199 et 256.

KITTEL, C. et KROEMER, H., “Thermal Physics”, Éditions W.H. Freeman and Company, 1998, p. 53.

http://www.sev.com.au/toonzone/twist/strips/twist260.asp

http://matin.math.unicaen.fr/~reyssat/laplace/#philo

Retour à la liste des chroniques