Piste rouge

Analyse de Fourier

(Le présent article fait intervenir des notions de calcul différentiel et intégral. Une connaissance de ces notions est nécessaire pour la compréhension)

Plusieurs branches des mathématiques ont été développées sans qu’on y trouve immédiatement des applications pratiques. Ce n’est souvent que beaucoup plus tard (souvent des dizaines d’années, voire plus) que nous trouvons un champ d’application physique à ces branches.

L’un de ces domaines est celui de l’analyse de Fourier. Afin d’approfondir ce domaine, nous vous citons ci-bas des passages du livre Analyse de Fourier et calcul opérationnel de M. Armel Mercier, professeur de mathématiques à l’Université du Québec à Chicoutimi. M. Mercier est l’un des professeurs les plus compétents que j’ai eu et je tiens à préciser que si les passages suivants contiennent des erreurs, elles me sont entièrement imputables.

Le mathématicien français Joseph Fourier (1768-1830) conjecturait qu’une fonction arbitraire, définie sur (-p, p), pouvait être représentée par une sommation de sinus et de cosinus. L’intérêt est que lorsqu’on exprime une fonction sous forme de sinus et de cosinus, on est plus apte à découvrir les propriétés de cette fonction car on peut l’analyser selon les propriétés des fonctions sinus et cosinus (identités trigonométriques). L’idée avait été préalablement connue par Leonhard Euler (1707-1783) et Jean le Rond d’Alembert (1717-1783), mais ces mathématiciens n’avaient pas vu les nombreuses applications que l’on pouvait y rattacher.

La conjecture de Fourier n’était pas acceptée par nombre de mathématiciens à son époque, dont Lagrange, Laplace et Legendre. Cependant, c’est grâce aux séries et aux transformations de Fourier qu’aujourd’hui, nous pouvons analyser des signaux radios nous provenant de l’espace et tenter ainsi de trouver un signal non-naturel.

Série de Fourier

Si :

t est dans l’ensemble R

T est la période de la fonction, i.e. f (t+T) = f(t) pour tout t dans l’ensemble R

La série trigonométrique suivante :

f(t) = a₀ / 2 +	∞	a_ncos nwt + b_nsin nwt avec w = 2π/T
	Σ
	n=1

est appelée une série de Fourier.

Les coefficients a₀, a_n et b_n se calculent à l’aide des formules d’Euler :

a₀ = 2 / T ∫	d+T	f(t) dt
	d

a_n = 2 / T ∫	d+T	f(t) cos nwt dt
	d

b_n = 2 / T ∫	d+T	f(t) sin nwt dt
	d

où d est un nombre réel quelconque.

Ex : Onde en créneau

La pression de l’air au niveau de l’oreille résultant d’un battement périodique des mains peut être approchée par une onde en créneau.

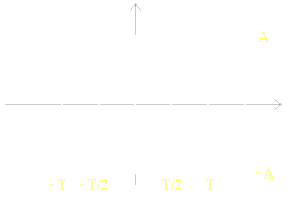
Dans ce problème, nous avons une fonction périodique de période T, d’où en posant d = -1/2 T, on a, pour n ≥ 0 (w = 2π / T)

a_n	= 2 / T		∫	T/2	f(t) cos nwt dt
				-T/2
	= 2 / T	{	∫	0	-A cos nwt dt +	∫	T/2	A cos nwt dt	}	= 0
				-T/2			0

D’autre part, pour n ≥ 1,

b_n	= 2 / T ∫	T/2	f(t) cos nwt dt
		-T/2

	= 2 / T { - A ∫	0	sin (2nwπt) dt + A ∫	T/2	sin (2nwπt) dt } = 0

	0	si n est pair
= 2A/np(1 - cos np) =
	4A / np	si n est impair

On peut écrire

f(t) = (4A / π)	∞	sin ( ( (2n +1) 2πt / T) / 2n + 1)
	Σ
	n=0

Ainsi, il est plus aisé de trouver les propriétés de la fonction (convergence, spectre de fréquence, etc.) sous cette forme que sous sa forme initiale.

Intégrale de Fourier

Si les séries de Fourier expriment un phénomène périodique en une sommation de sinus et de cosinus, les intégrales de Fourier, elles, peuvent exprimer une fonction non-périodique de façon analogue aux séries de Fourier. On fait tendre la période T vers l’infini (puisque la fonction n’est pas périodique).

Si f est une fonction régulière par morceaux sur tout intervalle de longueur finie et si

∫	∞	\|f(t)\| dt existe, alors pour tout t ϵ (-∞,∞), nous avons
	-∞

f(t) = 1 / p	∫	∞	∫	∞	f(s) cos w(s - t) ds dw
		0		-∞

cette expression est appelée intégrale de Fourier pour la fonction f.

On peut aussi écrire cette intégrale sous forme exponentielle,

f(t) = 1 / 2p	∫	∞	∫	∞	f(s) e^-i^{w(s - t)} ds dw
		0		-∞

Transformée de Fourier

Pour plusieurs fonctions, l’intégrale de Fourier est très difficile à évaluer. C’est pourquoi nous la fractionnons en définissant ce que l’on appelle la transformée de Fourier. La transformée de Fourier a l’avantage d’être en fonction de la fréquence w et non du temps t. Pour plusieurs applications pratiques, une expression en fonction de la fréquence est beaucoup plus utile.

D’après la formule de l’intégrale de Fourier sous forme exponentielle, on a

f(t) = 1 / 2p	∫	∞	(∫	∞	f(s) e^-i^ws ds	)	eⁱ^wt dw
		-∞		-∞

d’où en posant

f(w) =	∫	∞	f(s) e^-i^ws ds
		-∞

on obtient

f(t) = 1 / 2p	∫	∞	f(w) eⁱ^wt dw
		-∞

La fonction F(w) est appelée transformée de Fourier de f(t) et la fonction f(t) est appelée la transformée inverse de Fourier de F(w).

Transformée de Fourier discrète (TFD)

Pour calculer la transformée de Fourier à l’aide d’un calculateur, on utilise la transformée de Fourier discrète (TFD). Au lieu d’avoir une fonction pour tout x, nous avons seulement les valeurs de f en un nombre fini de points f(x₁), f(x₂), …, f(x_n). Les points sont supposés à intervalle régulier, T disons. Si notre échantillonnage commence avec x1 = 0, la suite de points formée de l’échantillonnage devient 0, 2T, …, (n-1)T. Par analogie à la transformée de Fourier de f, la transformée de Fourier discrète de f est définie comme

f(k) =	N-1	f(n) e^{-i (2}^{π / n)nk} k = 0,1,...,N-1
	Σ
	n=0

La transformée inverse de Fourier discrète est définie de façon semblable

f(n) = 1 / N	N-1	f(k) eⁱ⁽²^{π / N)nk} n = 0,1,...,N-1
	Σ
	k=0

Sans ordinateur, le calcul numérique d’une transformée de Fourier discrète est plutôt pénible, car on doit calculer manuellement un grand nombre de facteur, ce qui est décourageant. La quantité de calculs dépend essentiellement du nombre de points nécessaires à la description de l’onde : le nombre d’additions est de l’ordre du nombre de points, alors que le nombre de multiplications est égal au carré du nombre de points. Ainsi, l’analyse d’une onde décrite par 1000 points à intervalles réguliers nécessite environ 1000 additions et un million de multiplications.

Transformée de Fourier rapide (TFR)

Pour que les calculs numériques soient plus accessibles, on a mis au point des ordinateurs et des programmes pour exécuter des techniques nouvelles d’analyse de Fourier. L’une d’elles, la transformée de Fourier rapide (TFR), ou en anglais Fast Fourier Transform (FFT), fut développée en 1965 par James Colley, du Centre de recherche Thomas Watson d’IBM, et John Tukey, des Laboratoires Bell Telephone. La transformée de Fourier rapide mérite son nom parce qu’elle réduit de façon appréciable le nombre de multiplications.

Il est à noter que le programme seti@home fait effectuer par votre ordinateur des transformées de Fourier rapides sur les signaux radio captés par le radio télescope d’Arecibo.

On sait que la transformée de Fourier discrète est

f(k) =	N-1	f(n) e^{-i (2}^{π / n)nk} k = 0,1,...,N-1
	Σ
	n=0

Introduisons la fonction W_N = e ^-(2^{πi / N)}, alors la transformée de Fourier discrète devient

f(k) =	N-1	f(n) W_N^nk k = 0,1,...,N-1
	Σ
	n=0

On peut aussi l’exprimer sous la forme matricielle suivante :

F(N-1)

W_N^N-1

...

W_N⁽^N-1)(N-1)

f(N-1)

F(1)

W_N

...

W_N^N-1

f(1)

F(2)

W_N²

...

W_N²⁽^N-1)

f(2)

...

F(N-1)

W_N^N-1

...

W_N⁽^N-1)(N-1)

f(N-1)

La matrice carrée d’ordre N présente des particularités évidentes : les lignes et les colonnes de même indice ont les mêmes éléments et ces éléments sont des puissances d’un nombre de base W_N tel que W_N ^N = 1. On peut alors envisager des simplifications importantes conduisant ainsi à des algorithmes rapides. Un cas très intéressant est celui où N est une puissance de deux. Dans ce cas, on est conduit à des algorithmes peu complexes et qui sont particulièrement efficaces. Par exemple, lorsque N = 2^π, on peut montrer que le nombre de multiplications requis pour évaluer la transformée de Fourier rapide est de N / 2 log₂ N. Par exemple, si N = 1024 = 2¹⁰, alors la TFR requiert 5 120 multiplications alors qu’il faut 1 048 576 multiplications pour la TFD.

Il y a plusieurs autres développements en mathématiques ont menés à des découvertes stupéfiantes. Par exemple, les nombres complexes, la géométrie fractale, les dérivées fractionnaires et le nombre d’or relié à la suite de Fibonnaci. Lorsque des domaines aussi abstraits que ceux-ci trouvent résonance dans la réalité, il est difficile de croire que les mathématiques ne sont qu’une invention de l’esprit humain.

Commentaires ? Suggestions ? Infarctus ? Écrivez-les moi à svilleneuve@cegep-chicoutimi.qc.ca

Références

MERCIER, Armel (1994), « Analyse de Fourier et calcul opérationnel », Publié par le Département d’informatique et de mathématique, UQAC, 244 pages

Retour à la liste des chroniques